主成分分析のbiplotと相関係数の関係について
1. 主成分分析
まずは主成分分析をしてみる。次のcolaboratryを参照してほしい。
https://colab.research.google.com/drive/1Te2yuuMpqYy_UkQxinWAAZ-kxtcPVZpL?usp=sharing
ワインのデータから、 'Color intensity', 'Flavanoids', 'Alcohol', 'Proline'のデータについて、scikit-learnのPCAモジュールを用いて主成分分析を行っている。
なお、主成分分析とデータについては主成分分析を Python で理解するを参照した。
colaboratryの1章で、主成分分析をしてbiplotを実行している。

また、各変数の相関係数は次のようになった。
| Color intensity | Flavanoids | Alcohol | Proline | |
|---|---|---|---|---|
| Color intensity | 1.000000 | -0.172379 | 0.546364 | 0.316100 |
| Flavanoids | -0.172379 | 1.000000 | 0.236815 | 0.494193 |
| Alcohol | 0.546364 | 0.236815 | 1.000000 | 0.643720 |
| Proline | 0.316100 | 0.494193 | 0.643720 | 1.000000 |
このbiplot上の変数同士の角度と、相関係数にはなにか関係があるだろうか?例えば、角度が0度に近ければ相関が高く、90度近ければ相関が低いと言えるだろうか?
colaboratryの2章で相関係数とbiplotの角度の$\cos$についてプロットしてみている。

線形な関係がありそうである。
相関係数、主成分分析、どちらも基本的な線形代数の手法を用いて導くことができる。この関係について調査する。
2. 分散共分散行列と相関行列の関係
データ数$n$の2種類のデータ$x,y$をどちらも平均$0$、不偏分散を$1$に標準化しておく 相関係数$r _ {xy}$は次のように変形できる。
となる。ただし$s _ {xy}$は不偏共分散で、次のように計算する。
また、データを標準化しているので、
となることを用いた。
よって、標準化された、$m$種類のデータについて$n$個観測した、$n$行$m$列のデータ$X$を次のように計算した不偏分散共分散行列は相関係数行列と等しくなる。
3. 主成分分析と固有値分解
主成分分析は分散共分散行列を固有値分解することでできる。主成分分析について詳しくは↓の資料、もしくは他の書籍などを参照。
この時、固有値は大きい順に並び替えてあるものとする。 そして、元のデータを主成分に変換したい場合は$XV _ {pca}$を計算する。
4. 寄与度プロット(biplot)の角度と相関係数
PCAでは、第一主成分と第二主成分における観測変数の寄与度をプロットするbiplotによって、データ全体の傾向を掴もうとすることがよく行われる。そのときの寄与度プロットでの$i$列目と$j$列目の観測変数の矢印同士の角度を$\theta _ {ij}$とすると、その余弦$\cos{\theta _ {ij}}$はベクトル$\pmb{u} _ i$と$\pmb{u} _ j$の第1成分、第2成分を成分としたベクトル$\pmb{u}' _ i$、$\pmb{u}' _ j$の内積を$\|\pmb{u}' _ i\|\|\pmb{u}' _ j\|$で割ったものとなる。つまり、
一方、$i$列目と$j$列目の変数の相関係数は
である。この2つは等しくない。しかし、もし仮にPC1とPC2の2つの分散がすべての分散のかなりの割合を占めていて、PC3以降の分散が無視できる場合、
となる。PC1とPC2における観測変数の寄与度にそれぞれPC1とPC2の標準偏差をかけた座標でプロットした時、つまり$(\sqrt{\lambda _ 1}u _ {i1},\sqrt{\lambda _ 2}u _ {i2})$、$(\sqrt{\lambda _ 1}u _ {j1},\sqrt{\lambda _ 2}u _ {j2})$などとプロットした時の角度$\theta'$について考える。このプロットの方法を修正biplotと呼ぶことにする。このとき、修正biplotのベクトルの長さ$\|\pmb{u}''\|$がどれもほぼ同じ$(\approx l)$であれば、
となり、$\cos{\theta' _ {ij}}$は相関係数$r _ {ij}$と比例する。また、ベクトルの長さが一定以上あり、$\cos{\theta' _ {ij}}$が0であれば、つまりベクトル同士が90度であれば、相関は0といっていい。
5. 具体例
5.1 ワインデータ
先程のワインの例をもう1度見てみよう。
https://colab.research.google.com/drive/1Te2yuuMpqYy_UkQxinWAAZ-kxtcPVZpL?usp=sharing
colaboratryの3章で固有値、固有ベクトル、そして分散の割合を確認している。
固有値(=分散)$\lambda _ i$は次のようになっていた。
| 固有値(分散) | |
|---|---|
| PC1 | 2.134122 |
| PC2 | 1.238082 |
| PC3 | 0.339148 |
| PC4 | 0.288648 |
そして固有ベクトル$V _ {pca}$、pca.components_.Tは次のようになっていた。
| PC1 | PC2 | PC3 | PC4 | |
|---|---|---|---|---|
| Color intensity | 0.409416 | 0.633932 | 0.636547 | -0.159113 |
| Flavanoids | 0.325547 | -0.725357 | 0.566896 | 0.215651 |
| Alcohol | 0.605601 | 0.168286 | -0.388715 | 0.673667 |
| Proline | 0.599704 | -0.208967 | -0.349768 | -0.688731 |
この表の1行それぞれが$\pmb{u}$ベクトルである。
分散の割合は次のようになっていた。
| 割合 | |
|---|---|
| PC1 | 0.533531 |
| PC2 | 0.309520 |
| PC3 | 0.084787 |
| PC4 | 0.072162 |
PC1とPC2の分散が全体の約84%の分散を占めている。
また、修正biplotでのベクトルのnormは次のようになっていた
| 修正biplotでのベクトルの長さ | |
|---|---|
| Color intensity | 0.924809 |
| Flavanoids | 0.936794 |
| Alcohol | 0.904300 |
| Proline | 0.906416 |
ベクトルの長さがだいたい同じである。よって、修正biplotの方法でプロットすれば、角度の$\cos$が相関係数が多少比例するはずである。
colaboratryの5章で通常のbiplotと修正biplotを比較している。

PC1の分散がPC2より大きい分、修正biplotでは通常のbiplotに比べて横に引き伸ばされている。
そしてcolaboratryの6章で相関係数と通常のbiplotと修正biplotそれぞれでの角度の$\cos$をプロットしている。修正biplotでは相関係数と$\cos$がほぼ比例していることがわかる。

5.2 すべてのワインデータ
colaboratryのAppendix 2章でワインデータについて13ある全ての観測変数でPCAを行っている。修正biplotは次のようになった。

相関係数と$\cos$の比較は次のようになった。

このときPC1とPC2の分散が全体の約56%の分散を占めてた。
つまりこの場合、PC1とPC2の分散が全体の大部分を占めていて、修正biplotのベクトルの長さがだいたい同じであるので相関係数と修正biplotの角度の$\cos$がだいたい比例している。
5.3 ランダムなデータ
colaboratryのAppendix 3章で観測変数が10あるランダムなデータを生成してPCAを行っている。1変数目、2変数目、3変数目同士、そして4変数目、5変数目、6変数目同士の相関が高くなるようにした。それ以外の相関は低く設定してある。修正biplotは次のようになった。

相関係数と$\cos$の比較は次のようになった。

このときPC1とPC2の分散が全体の約49%の分散を占めてた。
つまりこの場合は、PC1とPC2の分散が全体の大部分を占めてはいるが、修正biplotのベクトルの長さがばらばらなので相関係数と修正biplotの角度の$\cos$は比例しない。
6.結論
- PC1とPC2の分散が全体の大部分を占めていて、修正biplotのベクトルの長さがだいたい同じである場合、相関係数と修正biplotの角度の$cos$はほぼ比例する。
- PC1とPC2の分散が全体の大部分を占めていて、修正biplotのベクトルの長さが少しでもあり、ベクトル同士の角度が90度に近いものは相関は小さい。
7. 相関を見たいときは
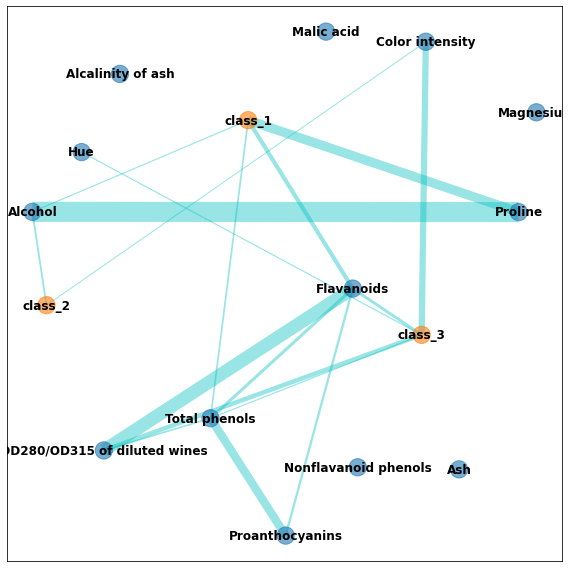
相関を見たいときは、次のようにheatmapやグラフ(ネットワーク図)で表したほうがいいと思われる。
https://colab.research.google.com/drive/1Ga7XhsNVs7H8zO7W5O--rotPiKxDUBLV?usp=sharing
クラス分類をone-hot encodingにして相関を取り、相関係数の大きさをedgeの太さにしてグラフ化した。